I threw out a goofy story one day a few weeks ago to get the kids to manipulate radicals properly, and it seemed to help some kids, so I thought I'd share ... and I guess I'll share in building up order instead of the order in which it happened.
I make sure to ask a student (or class) what this means:
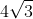
. I get a variety of answers:
* I don't know
* 4 times
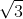
?
* are you asking me?
* what?
So then I look suddenly across the room, "Look over there! What's that?". They look. "Just see those 4 cute little
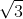
s running around!" And I go on to describe that you're just counting in shorthand how many there are.
And then if there's a problem like
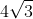
+
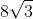
, I expand the story: "... and over by the door, 8 more sexy
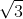
s just joined the party! How many are in the room now?"
I guess it sticks with SOME of the students because today we had a problem like: (12)(
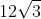
) and someone was wondering how to multiply it. So I asked: "what does
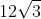
mean?". Pretty quickly someone answered: you have 12 little
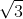
s running around. And then we were able to finish the problem (and you have 12 sets of those 12, so .....
My next goal (someday) is to have them do a dramatic interpretation or story or SOMETHING emotional about
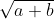
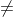
+
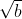
. I've read that things that pack an emotional punch in some way stick better in your head. Or maybe it's just the punching part ....
I was searching for such a thing for a very long time.
ReplyDelete